
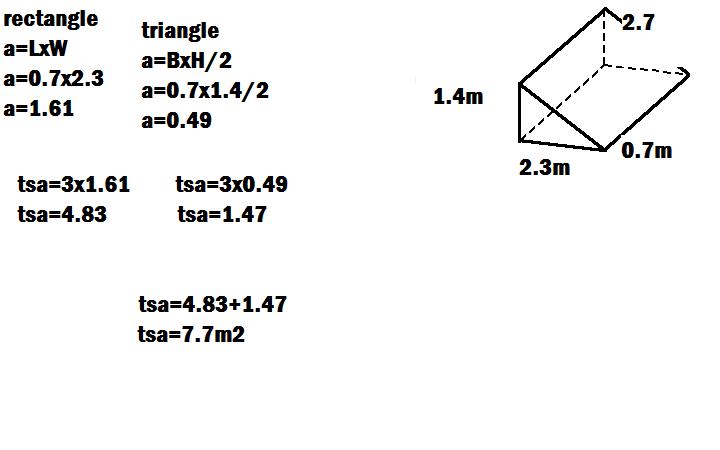
#Right angle triangular prism formula plus#
Well, that gets us x squared is equal to one plus five, right? Square root of five squared is just five.
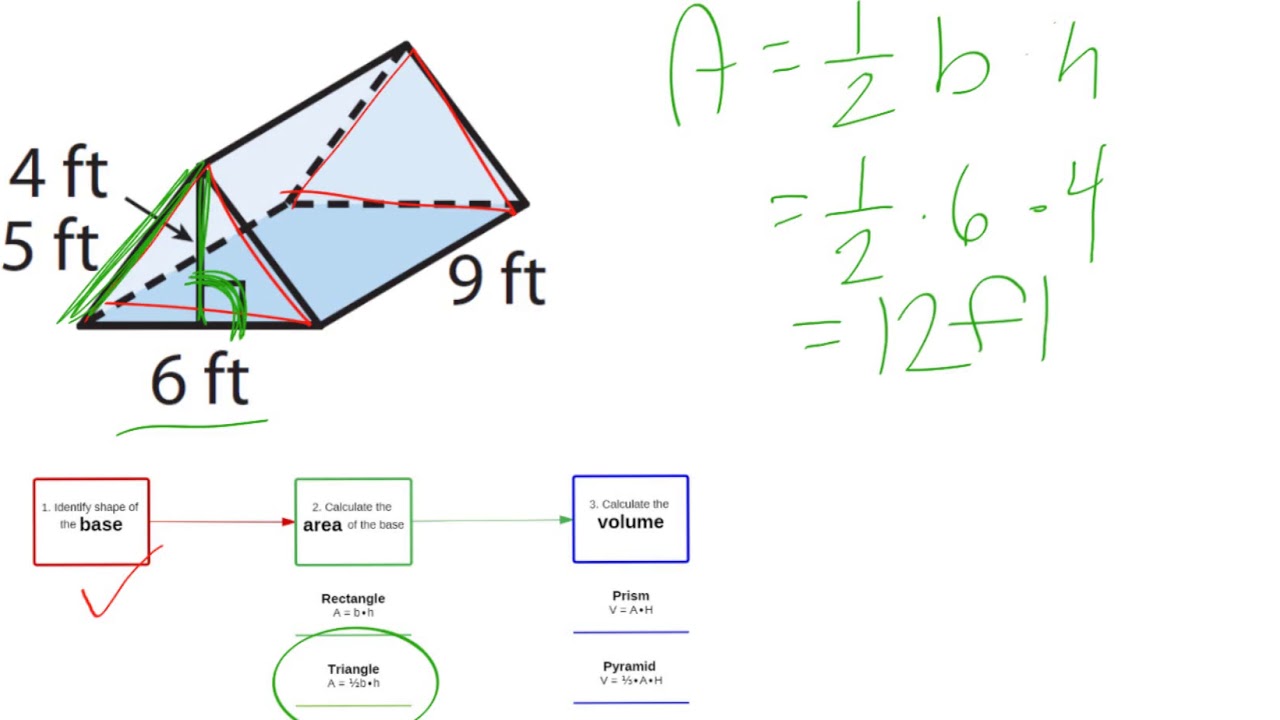
Root of five squared, plus square root of five squared. Which is just, I'll just write it one squared plus square This is a right triangle, so we can apply the Pythagorean theorem again. So I'll draw that, that is of length one. Well, I'd say we're talkin' about this height right over here is length one. And then we have a height, Let me do it, looks like it's in a. So we have this side is the square root of five. Length one is perpendicular to this entire plane. Of visualization practice to visualize this right. So this length right over here is the square root of five, We can write a squared is equal to five, or we could say that a is equal to the principal root of five. One squared plus two squared, which of course, isĮqual to one plus four, which is equal to five. We know that the hypotenuse squared is going to be equal to one squared, one squared plus two squared. And then this right over here is going to be the sameĪs this right over here, which is going to be of length two. So this right over here is the same thing as this right over here. We know that this length is half of this side right over here, so that's going to be one. So if we look at it in two dimensions, If we look at it in two dimensions, it would look something like this. Solution: First, we need to calculate the area of the triangular base. Example: Find the volume of the following right prism. Solution: Volume Ah 25 cm 2 × 9 cm 225 cm 3. How do we figure out length a? Well let's just take it out and look at it in two dimensions. Worksheet to calculate volume of prisms and pyramids. How do we figure out, how do we figure out I dunno, let me call this length. That length and the one are the two non-hypotenuse sides of a right triangle. Well why is this length interesting? Well if we know that length, that length forms a right triangle. We should be able toįigure out this length. Actually, I'll keep it in this color 'cause this color's easy to see. We should be able to figure out this length. Well how does that help us? Well using that information, Two, then each of these, this is going to be one, and this is going to be Prism, so this length is going to be the same So if this whole thing is two, and we see it right over here. Thing we can figure out, we can figure out what That's going to be two,Īnd that's going to be two. So half way, this is going to be, I'll write it with perspective. Well this entire length right over here is length four. This point right over here it's half way in this direction and half way in this direction.

Realize, well okay this point, this base right over here, The Pythagorean theorum, maybe more than once.
So with that in mind, I encourage you to pause the video and see It's perpendicular to the top of the rectangular prism. Is that this red line, that's one unit long, it is perpendicular, it is perpendicular to this entire plane. And so I encourage you to pause this video and try to think about it on your own. What is that length? And we will call that, These edges right over here? So either that one, or But our goal here, our goal here, is to figure out what is the length? What is the length of one of
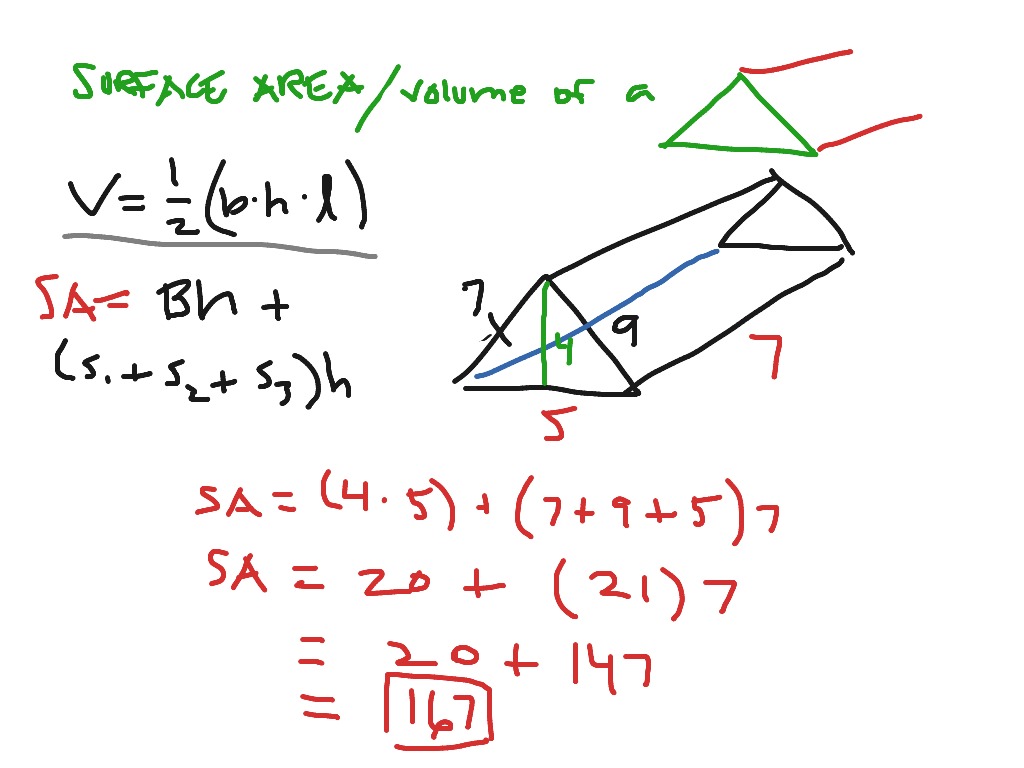
And this hasn't beenĭrawn completely to scale, and kind of the perspective Of its base right over here, and you go to the top, this height right over here is one unit. And then on top of that, on top of that, we have what you couldĬall a right pyramid, where the height of this right pyramid, so if you start at the center Guess we could say tall, four units wide, and then four units long. That rectangular prism, it's three units I All cross-sections parallel to the base faces are the same triangle.Īs a semiregular (or uniform) polyhedron Ī right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares.- So we have an interesting shape right over here. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.Įquivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). A right triangular prism has rectangular sides, otherwise it is oblique. In geometry, a triangular prism is a three-sided prism it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.


 0 kommentar(er)
0 kommentar(er)
